Three Distributions each of 100 Members and a Standard Deviation of 4.5 units: Mathematics Assignment, SUSS, Singapore

1 . Three distributions each of 100 members and a standard deviation of 4.5 units are located with means at 12.1, 17.1, 22.1 units respectively. Showing details in the work, determine the standard deviation of the distribution obtained by combining the three.

2 . In a certain institute, it is known that 15% of all students score grades “A” in Statistics 101. Four male students and five female students are selected at random from the Statistics 101 class. With appropriate assumption(s), compute the probability that in the selected group

(a)  3 students in the selected group score “A”;

(b)  1 male and 2 female students score “A”;

(c)  at most 2 female students and at least 1 male student score “A”.

3 . Certain devices are received at an assembly plant in batches of 50. The sampling scheme used to test all batches has been set up in the following way. One of the 50 devices is chosen randomly and tested. If it is defective, all the remaining 49 items in that batch are returned to the supplier for individual testing; if the tested device is not defective, another device is chosen randomly and tested. If the second item is not defective, the complete batch is accepted without any more testing; if the second device is defective, a third device is chosen randomly and tested. If the third device is not defective, the complete batch is accepted without any more testing, but the one defective device is replaced by the supplier. If the third device is defective, all remaining 47 items in that batch are returned to the supplier for individual testing.

The receiver pays for all initial single-item tests. However, whenever the remaining devices in a batch are returned to the supplier for individual tests, the costs of this extra testing are paid by the supplier. If a batch is returned to the supplier, the superintendent must ensure that the receiver is sent 50 items that have been tested and shown to be good. We ignore the cost of subsequent tests for replacement items.

Assume that the superintendent accepts the results of the receiver’s tests. Each device is worth $60 and the cost of testing is $10 per device.

Consider a particular batch that contains 12 defective items. Showing your full workings for the following clearly,

(a)  compute the probability that the batch will be accepted;

(b)  compute the expected cost to the supplier of the testing and of replacing defectives;

(c)  of the 12 defective items in the batch, derive the expected number which will be accepted.

4. (a) For a random variable, W, show that

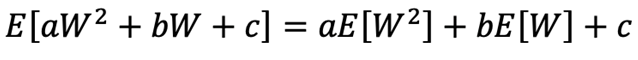
where a, b and c are constants.

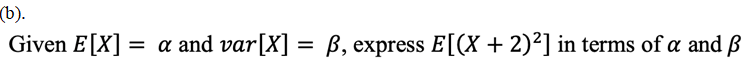
5. The support of a uniformly distributed random variable W is
S = {1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 15, 16}.

Compute, showing your detailed working:

(a)  E[W] and var[W];

(b)  P[W > 5 | W is odd].

6.

a. The random variable X has a Poisson distribution and is such that P[X=2] = 3P[X=4]. Evaluate the values of

1. (i)  P[X=0];
2. (ii)  P[X≥4].

b. The telephone exchange inside an office building has a number of outside lines of which, on average, 3 are being used at any instant. Assuming that the number of lines in use at any instant follows a Poisson distribution. Applying the Poisson model, evaluate the minimum number of outside lines required if there is a probability of more than 0.9 that, at any given instant, at least one of the lines is not being used.