Learning Objectives
- Determine the criterion for grid convergence for a laminar one-dimensional channel flow
- Solve nonlinear one-dimensional channel flow for non-Newtonian fluid
Problem 1
Apply the finite volume technique to discretize and solve one-dimensional fully developed laminar flow between two horizontal parallel plates governed by
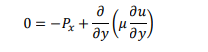
𝑢𝑢 is the velocity, 𝑃𝑃𝑥𝑥 is the pressure gradient and µ is the viscosity. In conservative form, this can be written as
In your solution show:
• A sketch for the cells, clearly marking faces and nodes for internal and boundary cells.
• Apply the linear approximation and use Dirichlet (velocity specified) boundary conditions to determine the approximate equations for internal and boundary cells.
• Compute the velocity distribution and compare your result with the exact solution, by adapting one of the uploaded codes. The number of grid cells is left up to you to determine. The solution must be grid converged.
For the numerical solution, let 𝑃𝑃𝑥𝑥 = 2µ, ℎ = 0.1, 𝑢𝑢(0) = 𝑢𝑢1 = 0.01, & 𝑢𝑢(ℎ) = 𝑢𝑢2 = 0. For grid convergence, you may define an error norm , and require that the error is less than 0.01𝑢 = 0.01 × 0.01. The exact solution is given by
Problem 2
Apply the finite volume technique to discretize and solve one-dimensional fully developed laminar non-Newtonian flow between two horizontal parallel plates governed by,
𝑢𝑢 is the velocity, 𝑃𝑃𝑥𝑥 is the pressure gradient. For non-Newtonian fluids, the viscosity µ𝑒𝑒 depends on the flow strain rate, which for one-dimensional fully developed flow is approximated by,
where 𝜇𝜇𝑜𝑜, 𝜅𝜅 are constants. Non-Newtonian fluids exist in several important applications, particularly in fluids using in printing, molten plastics used in 3D printers and most important for us, in blood and rheological flows. For more insight, you can check
https://www.rheosense.com/applications/viscosity/newtonian-non-newtonian
to learn more about the shear thinning and thickening effects. As this is a non-linear problem, it is highly recommended to follow the suggested algorithm
Buy Custom Answer of This Assessment & Raise Your Grades
1. Solve the case for the Newtonian fluid as a baseline. You already have the solution to problem 1. Call the solution 𝑢1
2. Solve the non-linear problem. Note you need to compute the viscosity 𝜇𝜇𝑒𝑒 on the faces of the volumes. To do so, use the velocity computed in step 1, and determine the viscosity on the north and south face. After solving, call the solution 𝑢𝑢2.
3. Compute the residual (change in the solution from steps 1 and 2) to determine if you have converged. For the residual use the code “residual = norm(u1-u2,2)” which calculate the difference between two vectors 𝑢𝑢1, 𝑢𝑢2 and obtains the 𝐿𝐿2 norm (standard deviation).
4. Rename the solutions, 𝑢𝑢1 = 𝑢𝑢2ot add a terminating condition at this stage. You already have a code in the distribution package for a non-linear diffusion problem that you can adapt.
Regardless adding an outer loop for the iteration should not be difficult. To make life simpler, use 𝑁𝑁 = 25 grid points, 𝑃𝑃𝑥𝑥
5. Repeat step (2)-(4) 50 times. In practice we stop after convergence, however, to simplify the programming for you, I will n = 2µ o, ℎ = 0.1, 𝑢𝑢(0) = 𝑢𝑢(ℎ) = 0
To make life simpler, use 𝑁𝑁 = 25 grid points, 𝑃𝑃𝑥𝑥 = 2µ o, ℎ = 0.1, 𝑢𝑢(0) = 𝑢𝑢(ℎ) = 0. Solve for 𝜅𝜅 = −0.3, 0, 0.3. Plot the residuals versus the number of iterations, and the normalized velocity (take your solution 𝑢𝑢2 and divide by the mean of 𝑢𝑢2) versus the channel height. The output should look like the following plots
