| University | Kaplan University (KU) |
| Subject | Math |
Assignment Details:
Question 1: (a) What the following parametric equations express: x = 2t, y = 3t – 4, -1≤ t≤2;
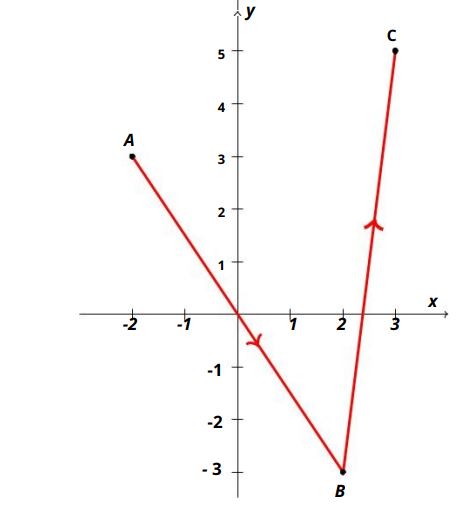
(b) write the parametric equations of the linear path A B → → C of the schema below, where A ( -2, 3) B (2, – 3) and C (3, 5) such that the parameter t takes values from [0, 2].
(c) express the parametric equations of the top half of the ellipse (x-1)^2 /4 + (y-2)^2 /9 = 1.
Question 2: Let the function f (x, y, z) = x – zy. Find the contour integral of f (x, y, z) from the point A(1, 0, 0) to the point B (0, 1, π/2) along the curve C, when the curve C is:
(A) the line segment that connects the A, B
(B) the arc of the helix with parametric equations x = cos t, y = sin t, z = t.
Is this contour integral independent of the path followed?
Question 3: Calculate the contour integral of F ( x, y) = ( – y, x) on the upper half of a circle centered at (0, 0) of radius 4, anti-clockwise.
Buy Custom Answer of This Assessment & Raise Your Grades
Question 4: A point performs two complete rotations, anti-clockwise, on a circle in the plane 0xy with (center 0, 0) and radius 3 under the influence of the force field F(x,y,z) = ( 2x – y + z, x + y – z2, 3x – 2y + 4z) find the work produced.
Question 5: A thin homogeneous string wire of density d = 1 lies on the curve C described by the function r ( t) = (t – sin t, 1 – cos t, 1) 0 ≤ ≤ t 2 π. Find the center of mass.
Question 6: Given the surface of the hyperboloid of one sheet x^2 + y^2 – z^2 = 1.
(a) Find a parameterize the monochonou hyperboloid.
(b)Determine the area of the surface struck by the monochono hyperboloid levelsz = – 1 and z = 1.
Question 7: Calculate the surface integral of the vector field F (x, y, z) = x3i + yx2j + zx2k on the surface S which divides vertically the circular cylinder x2+ y2= p2 p>0 the levels z = 0 and z = a, a> 0. The unit normal vector points towards the outside of S.
Question 8: Given F (x, y, z) = M(x, y, z)i + N(x, y, z)j + P(x, y, z)k and G( x, y, z) = xi + yj + zk vector fields. Prove that:
(a) rot ( v × G) = 2 v for each vector v = (a, b, c), where a, b, c ∈ R.
(b) If ∇ × F = 0, then ∇ · ( F × G) = 0.
Question 9: Given the vector field F ( x, y, z) = (sin(yz), xz cos(yz), xy cos(yz)).
(a) Prove that the vector field F It is conservative.
(b) Find the scalar potential function f for field F.
Question 10: Verify the Green theorem for the vector field F (x, y) = (xy2x + y) and area D bounded by the parabola y = x2 and the straight y = 2x.
Are you having trouble to solve out your math assignment questions? Then hire math homework helper of Singapore Assignment Help and get the quality solution for your maths homework and secure A+ grade anytime in Kaplan University.
Looking for Plagiarism free Answers for your college/ university Assignments.
- NUR3015 Health and Social Policy Summative Assignment Report 2025/26 | SIT
- PS5009MKT Digital Business Assessment Coursework | Coventry University
- 5007MKT Marketing Insight Assignment Coursework 2 – Coffee Shop Industry | Coventry University
- HL3044 The Legends of King Arthur Assignment Semester 1, AY2025-26 | NTU
- AVM343 Airport Design and Planning ECA July Semester 2025 | SUSS
- ICT239 Web Application Development End-of-Course Assessment – July Semester 2025
- BX2091 Tourism & Leisure Management Assessment Task 3, 2026 | JCU
- Project on Probability and Statistics using Matlab Assignment | NUS
- Health Economics and Policy Assessment Essay | Teesside University London
- BCAF004 Management Accounting & Finance Individual Assignment 1 AY 2025/2026 | TP

