What the following Parametric Equations Express: x = 2t, y = 3t – 4, -1≤ t≤2: Math Assignment, KU, Singapore

Assignment Details:

Question 1: (a) What the following parametric equations express: x = 2t, y = 3t – 4, -1≤ t≤2;

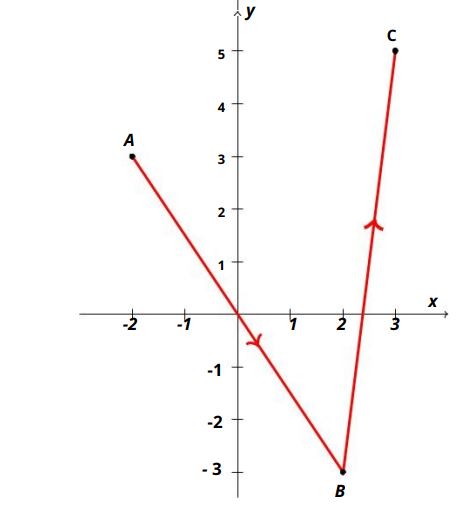
(b) write the parametric equations of the linear path A B → → C of the schema below, where A ( -2, 3) B (2, – 3) and C (3, 5) such that the parameter t takes values from [0, 2].

(c) express the parametric equations of the top half of the ellipse (x-1)^2 /4 + (y-2)^2 /9 = 1.

Question 2: Let the function f (x, y, z) = x – zy. Find the contour integral of f (x, y, z) from the point A(1, 0, 0) to the point B (0, 1, π/2) along the curve C, when the curve C is:

(A) the line segment that connects the A, B

(B) the arc of the helix with parametric equations x = cos t, y = sin t, z = t.

Is this contour integral independent of the path followed?

Question 3: Calculate the contour integral of F ( x, y) = ( – y, x) on the upper half of a circle centered at (0, 0) of radius 4, anti-clockwise.

Question 4: A point performs two complete rotations, anti-clockwise, on a circle in the plane 0xy with (center 0, 0) and radius 3 under the influence of the force field F(x,y,z) = ( 2x – y + z, x + y – z2, 3x – 2y + 4z) find the work produced.

Question 5: A thin homogeneous string wire of density d = 1 lies on the curve C described by the function r ( t) = (t – sin t, 1 – cos t, 1) 0 ≤ ≤ t 2 π. Find the center of mass.

Question 6: Given the surface of the hyperboloid of one sheet x^2 + y^2 – z^2 = 1.
(a) Find a parameterize the monochonou hyperboloid.

(b)Determine the area of the surface struck by the monochono hyperboloid levelsz = – 1 and z = 1.

Question 7: Calculate the surface integral of the vector field F (x, y, z) = x3i + yx2j + zx2k on the surface S which divides vertically the circular cylinder x2+ y2= p2 p>0 the levels z = 0 and z = a, a> 0. The unit normal vector points towards the outside of S.

Question 8: Given F (x, y, z) = M(x, y, z)i + N(x, y, z)j + P(x, y, z)k and G( x, y, z) = xi + yj + zk vector fields. Prove that:
(a) rot ( v × G) = 2 v for each vector v = (a, b, c), where a, b, c ∈ R.

(b) If ∇ × F = 0, then ∇ · ( F × G) = 0.

Question 9: Given the vector field F ( x, y, z) = (sin(yz), xz cos(yz), xy cos(yz)).
(a) Prove that the vector field F It is conservative.

(b) Find the scalar potential function f for field F.

Question 10: Verify the Green theorem for the vector field F (x, y) = (xy2x + y) and area D bounded by the parabola y = x2 and the straight y = 2x.