MME2121: A Training Model of an Overhead Gantry Crane is Shown in Figure 2: Engineering Dynamics Assignment, SIT, Singapore

1. Non-linear pendulum equation

To solve the non-linear ODE:

d²θ/dt² + g/l sinθ = 0

with initial conditions:

θ(0)=θο=0.2 rad; θ^º(0) = 0 rad/s

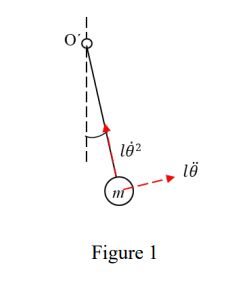
Let the length l = 9.81 m and g = 9.81 m/s2

1. Define the two states for the equation
2. Use ode45 to solve the equation for θ and dθ/dt or (𝜃𝜃̇) with respect to time for
   the initial angular displacements are given below. In all three cases, the initial
   angular velocity is 0 rad/s θο = 7.5°; θο = 30°; and θο =45°;

2. Linear pendulum equation. Use ode45 to solve the linearized equation given in A:  d²θ/dt² + g/lθ = 0

For the same initial conditions as A. Compare and comment on the results from the two problems.

Check your understanding by comparing sin(θ0) with θ0 i.e. at what angle will the solution of (A) and (B) differ by more than 10%? Note that θ0 must be expressed in radians,

3. A training model of an overhead gantry crane is shown in Figure 2. The trolley has a mass M = 20 kg. The position of the center of mass O’ of the trolley is x(t) from a fixed reference point O. A horizontal force f(t) is used to control the x movement of the trolley. A load of mass m = 2 kg is attached by a cable length l = 2 m to O’. The angle θ of the load cable from a vertical line is as shown, positive counterclockwise.

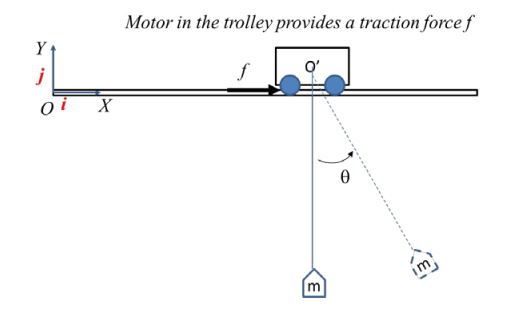
Figure 2

• Draw the FBD and KD for the trolley and the load. Let T represent the tension in the cable. State any necessary assumptions that you need to make.
• If your FBD and KD are correct, you should get for θ sufficiently small, a (linearised) simplified equation:

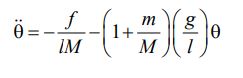
• The force to the trolley is f(t)=(A/wo²)•cos(2πt/to), where A is the maximum displacement of the trolley, wo=2π/to, and to is the period of the trolley motion.

Use Matlab ode45 to solve for the motion of θ in (1) And separately plot θ ( t ) and θ(t ) versus time for A = 2 and to = 1 second.

• The motion of the trolley is coupled to the motion of load by another ODE:

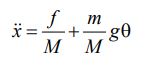
Try to solve (1) and (2) together.